ベタな方法
直線p1p2{p1(a,b)、p2(c,d)}とp3p4{p3(e,f)、p4(g,h)}の交点の座標は以下で表されます。
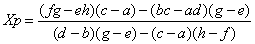
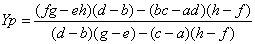
範囲内にあるかどうかの判定を加えれば線分と直線で交差するかどうかという判定も可能です。
// 線分(p1,p2)と直線(p3,p4)の交点を求める // 平行時は無限遠点が交点になっている(一応) int crossPoint ( const Dpoint3d &p1, const Dpoint3d &p2, const Dpoint3d &p3, const Dpoint3d &p4 Dpoint3d &ap1, // 交点 ) { double dev = (p2.y-p1.y)*(p4.x-p3.x)-(p2.x-p1.x)*(p4.y-p3.y) if ( !dev ) { ap1.x = INFINIT; ap1.y = INFINIT; ap1.z = 0; return 0; } double d1, d2; d1 = (p3.y*p4.x-p3.x*p4.y) d2 = (p1.y*p2.x-p1.x*p2.y) ap1.x = d1*(p2.x-p1.x) - d2*(p4.x-p3.x) ap1.x /= dev; ap1.y = d1*(p2.y-p1.y) - d2*(p4.y-p3.y) ap1.y /= dev; return isRange( p1 , p2, ap1) ? 1 : 0; }
よりクールな方法
一方、計算幾何学と地理情報処理にはより計算量が少ない方法として以下の方法が紹介されています。
線分P1P2とP3P4が交差するためにはPiの座標を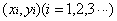 とあらわすと、
とあらわすと、
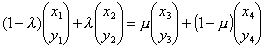
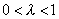
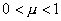
であれば良い。
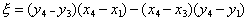
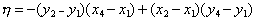
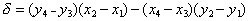
とすると
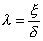
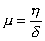
となります。交点の座標は
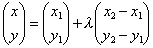
で求まります。
BOOL Cross_LineVSLine
(
XYZType L1,
XYZType L2,
XYZType L3,
XYZType L4,
XYZType &CrossP
)
{
double ksi, eta, delta;
double ramda, mu;
ksi = ( L4.y-L3.y )*( L4.x-L1.x ) -
( L4.x-L3.x )*( L4.y-L1.y )
eta = ( L2.x-L1.x )*( L4.y-L1.y ) -
( L2.y-L1.y )*( L4.x-L1.x )
delta = ( L2.x-L1.x )*( L4.y-L3.y ) -
( L2.y-L1.y )*( L4.x-L3.x )
ramda = ksi / delta;
mu = eta / delta;
if ( ( ramda >= 0 && ramda <= 1 ) && ( mu >= 0 && mu <= 1 ) )
{
CrossP.x = L1.x + ramda*( L2.x-L1.x )
CrossP.y = L1.y + ramda*( L2.y-L1.y )
//交点の高さ
CrossP.z = L1.z + ramda*( L2.z-L1.z )
return TRUE;
}
return FALSE;
}
参考文献
| 計算幾何学と地理情報処理 |
