多数の観測点がある場合
多数の観測点のデータで最小2乗法を用いてアフィン係数を計算する例です。
なお、最小二乗法を用いたアフィン係数は以下の計算式を使用しています。
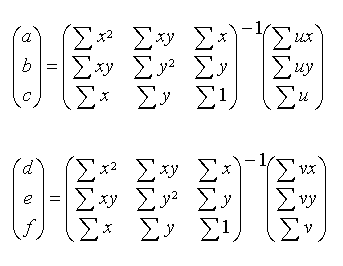
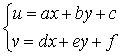
//アフィン変換係数を求める void calc_aff_coef ( vector< Dpoint3d > &orig, //STLを使用、観測値 vector< Dpoint3d > &trans, //変換後、photoCord型は写真座標を格納するクラス double aff_coef[6] //結果のアフィン係数を格納する ) { double **mat; double vect[6] = {0,0,0,0,0,0} double a; int i; mat = (double **)malloc( 3 * sizeof( double *) ); for ( i = 0; i < 3; i++ ) mat[i] = (double *)calloc( 3, sizeof( double ) ); for ( i = 0; i < orig.size(); i++ ) { a = (double )orig[i].x * (double )orig[i].x; mat[0][0] += a; a = (double )orig[i].x * (double )orig[i].y; mat[0][1] += a; mat[1][0] += a; a = (double )orig[i].x; mat[0][2] += a; mat[2][0] += a; a = (double )orig[i].y * (double )orig[i].y; mat[1][1] += a; a = (double )orig[i].y; mat[1][2] += a; mat[2][1] += a; mat[2][2] += 1; vect[0] += (double )orig[i].x * (double )trans[i].x; vect[1] += (double )orig[i].y * (double )trans[i].x; vect[2] += (double )trans[i].x; vect[3] += (double )orig[i].x * (double )trans[i].y; vect[4] += (double )orig[i].y * (double )trans[i].y; vect[5] += (double )trans[i].y; } //逆行列を計算する matinv( 3, (double **)mat ); aff_coef[0] = mat[0][0]*vect[0] + mat[0][1]*vect[1] + mat[0][2]*vect[2]; aff_coef[1] = mat[1][0]*vect[0] + mat[1][1]*vect[1] + mat[1][2]*vect[2]; aff_coef[2] = mat[2][0]*vect[0] + mat[2][1]*vect[1] + mat[2][2]*vect[2]; aff_coef[3] = mat[0][0]*vect[3] + mat[0][1]*vect[4] + mat[0][2]*vect[5]; aff_coef[4] = mat[1][0]*vect[3] + mat[1][1]*vect[4] + mat[1][2]*vect[5]; aff_coef[5] = mat[2][0]*vect[3] + mat[2][1]*vect[4] + mat[2][2]*vect[5]; for ( i = 0; i < 3; i++ ) free( mat[i] ); free( mat ); } //逆行列を計算する。結果は引数の配列に上書き //引用;「C言語によるアルゴリズム辞典」 void matinv(int n, double **a) { int i, j, k; double t, u, det; det = 1; for ( k = 0; k < n; k++ ) { t = a[k][k]; det *= t; for ( i = 0; i < n; i++ ) a[k][i] /= t; a[k][k] = 1 / t; for ( j = 0; j < n; j++ ) { if ( j != k ) { u = a[j][k]; for ( i = 0; i < n; i++ ) { if ( i != k ) a[j][i] -= a[k][i] * u; else a[j][i] = -u / t; } } } } } //アフィン変換を行う。 //引数 ;アフィン係数配列、Cord型変換元の座標 //戻り値;Cord変換後座標 //Cord型はxとyがあるのみの構造体 Cord aff_trans( double *aff_coef, Dpoint3d &point ) { Dpoint3d uv; uv.x = aff_coef[0]*point.x + aff_coef[1]*point.y + aff_coef[2]; uv.y = aff_coef[3]*point.x + aff_coef[4]*point.y + aff_coef[5]; return uv; }
縦、横の拡大率、回転、平行移動量が与えられた場合
縦・横の拡大・縮小率がそれぞれSH、SV、座標原点を中心として回転角がθである場合、変換は次式で表されます。
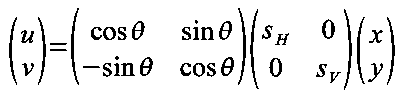
平行移動量をp、q とし、整理すると、上のアフィン変換の各係数は以下のようになります。
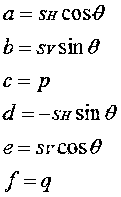
画像の場合
画像に対して幾何変換を行う場合は、平行移動量は画素の位置が負にならない条件で決定する必要があります。
変換後の座標値の最小値をUmin、Vminとすると、pとqは以下のようになります。
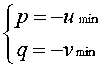
void calc_aff_coef ( double dHScale, double dVScale, double dAngle, int nInRow, int nInCol, int nOutRow, int nOutCol, double dCoef[6] ) { double dRad; //左上、右上、左下、右下の順の配列とする。 double dX[4]; double dY[4]; double dMinX, dMinY; int i; dRad = ( PI / 180 ) * dAngle; dCoef[0] = dHScale * cos( dRad ); dCoef[1] = dVScale * sin( dRad ); dCoef[3] = -1 * dHScale * sin( dRad ); dCoef[4] = dVScale * cos( dRad ); //変換後の4隅の座標を計算する dX[0] = 0.0; dX[1] = dCoef[0] * (double)(nInCol-1); dX[2] = dCoef[1] * (double)(nInRow-1); dX[3] = dX_TR + dX_BL; dY[0] = 0.0; dY[1] = dCoef[3] * (double)(nInCol-1); dY[2] = dCoef[4] * (double)(nInRow-1); dY[3] = dY_TR + dY_BL; //変換後の座標値の最大値と最小値を求める。 dMinX = dX[0]; dMinY = dY[0]; for ( i = 1; i < 4; i++ ) { if ( dMinX > dX[i] ) dMinX = dX[i]; if ( dMinY > dY[i] ) dMinY = dY[i]; } //変換後の座標が負にならないように平行移動量を決定する。 dCoef[2] = -1 * dMinX; dCoef[5] = -1 * dMinY; }
アフィン逆変換
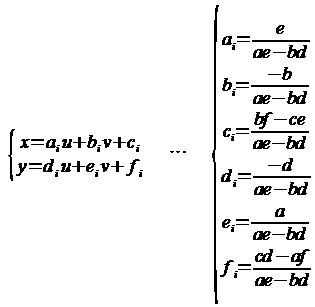
アフィン逆変換は以下の式で表されます。
2010年2月:数式が間違っていたのを修正
アフィン変換の画像への適用
アフィン変換を画像に適用する場合は、逆変換方式を適用するのが普通です。
あらかじめ、出力画像の範囲を求めておき、出力画像の全画素に対してアフィン逆変換を適用し、入力画像の範囲内であれば、入力画像上で内挿計算を行います。
内挿法によって、入力画像との内外判定が異なるので注意。最近隣内挿法では最近隣にあるピクセルが範囲内であればよく、共一次内挿法では周囲4ピクセルがすべて範囲内である必要があります。
/* 最近隣内挿法によるアフィン変換 daAffCoef : アフィン逆変換の係数 */ #define OUT_RANGE 255 /*範囲外は白塗りにする場合*/ void affin_trans_nearest ( BYTE *pbtIn, BYTE *pbtOut, int nInRow, int nInCol, int nOutRow, int nOutCol int nSample, double daAffCoef[6] ) { int i, j; int nRow, nCol; double dRow, dCol; for ( i = 0; i < nOutRow; i++ ) { for ( j = 0; j < nOutCol; j++ ) { dCol = daAffCoef[0] * (double)j + daAffCoef[1] * (double)i + daAffCoef[2]; dRow = daAffCoef[3] * (double)j + daAffCoef[4] * (double)i + daAffCoef[5]; nRow = (int)floor( dRow + 0.5 ); nCol = (int)floor( dCol + 0.5 ); //範囲のチェック if ( nCol < 0 || nCol >= nInCol || nRow < 0 || nRow >= nInRow ) { for ( k = 0; k < nSample; k++ ) { pbtOut[i*nOutCol*nSample+j*nSample+k] = OUT_RANGE; } } else { for ( k = 0; k < nSample; k++ ) { pbtOut[i*nOutCol*nSample+j*nSample+k] = pbtIn[nRow*nInCol*nSample+nCol*nSample+k]; } } } } } /* 共一次内挿法によるアフィン変換 */ void affin_trans_bilinear ( BYTE *pbtIn, BYTE *pbtOut, int nInRow, int nInCol, int nOutRow, int nOutCol, int nSample, double daAffCoef[6] ) { int i, j; int nRow0, nRow1, nCol0, nCol1; double dRow, dCol; double dRow0, dRow1, dCol0, dCol1; double dPix; for ( i = 0; i < nOutRow; i++ ) { for ( j = 0; j < nOutCol; j++ ) { dCol = daAffCoef[0] * (double)j + daAffCoef[1] * (double)i + daAffCoef[2]; dRow = daAffCoef[3] * (double)j + daAffCoef[4] * (double)i + daAffCoef[5]; //周囲4ピクセルの位置を特定 nRow0 = (int)floor( dRow ); nCol0 = (int)floor( dCol ); nRow1 = nRow0 + 1; nCol1 = nCol0 + 1; //範囲のチェック if ( nCol0 < 0 || nCol1 >= nInCol || nRow0 < 0 || nRow1 >= nInRow ) { for ( k = 0; k < nSample; k++ ) { pbtOut[i*nOutCol*nSample+j*nSample+k] = OUT_RANGE; } } else { //係数の計算 dCol0 = (double)nCol1 - dCol; dCol1 = dCol - (double)nCol0; dRow0 = (double)nRow1 - dRow; dRow1 = dRow - (double)nRow0; for ( k = 0; k < nSample; k++ ) { //ピクセル値の計算 dPix = dRow0*dCol0*(double)pbtIn[nRow0*nInCol*nSample+nCol0*nSample+k] + dRow0*dCol1*(double)pbtIn[nRow0*nInCol*nSample+nCol1*nSample+k] + dRow1*dCol0*(double)pbtIn[nRow1*nInCol*nSample+nCol0*nSample+k] + dRow1*dCol1*(double)pbtIn[nRow1*nInCol*nSample+nCol1*nSample+k]; pbtOut[i*nOutCol*nSample+j*nSample+k] = (BYTE)floor( dPix + 0.5 ); } } } } }
