回転した長方形を描画するときの豆知識です。
たいそうなものではありませんが、いざ作るとなると???となる自分用メモです。
3点指定で描画するには
まず任意の一辺を描画し、幅を指定して描画する場合は以下のようにします。
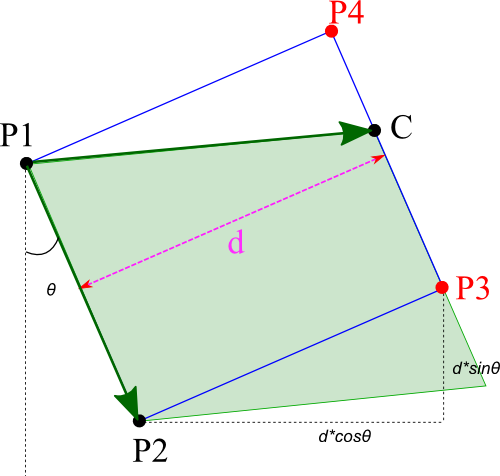
すなわち、図のように、任意の一辺P1P2を描画して、3点目のカーソルがCにあるときに、残りの2点(P3、P4)を求める方法です。
辺P1P2からCまでの距離は外積を使って求めるそうです。
すなわち、 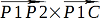 で図の薄緑の平行四辺形の面積が求まるので、
で図の薄緑の平行四辺形の面積が求まるので、
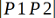 で割れば距離dが求まります。
で割れば距離dが求まります。
距離がわかれば、P3、P4の座標はそれぞれ図のように三角関数で求められます。
θの値は、Qt等のフレームワークで求める関数が用意されている場合はそれを使ってもいいですが、
無ければP1、P2の座標値からcosθ、sinθの値を簡単に求めることができます。
ただしその場合は線分P1P2と点Cの位置関係に応じて正負を適切に計算する必要があるでしょう。
以下のコードはQtを使った矩形描画の例です。
angle()とlength()が便利ですが、
それ以外は特にQtの機能は使っていません。
1: 2: // p01、p02がベースライン、pPosが点Cに対応しているものとする 3: QPointF p01, p02, pPos; 4: 5: // p03、p04が求めたい残りの2点 6: QPointF p03, p04 7: 8: // 外積 9: double dCrossProduct = p01.x()*p02.y() - p01.y()*p02.x(); 10: QLineF lineBase( p01, p02 ); 11: double dDist = dCrossProduct / lineBase.length(); 12: 13: // cosθ、sinθの計算 14: double dCos = qCos(qDegreesToRadians(lineBase.angle())); 15: double dSin = qSin(qDegreesToRadians(lineBase.angle())); 16: 17: // p03、p04を求める 18: // ここではベースラインから角度を求めているのでsinとcosが逆になっている 19: p03.setX( p02.x() + dDist*dSin ); 20: p03.setY( p02.y() + dDist*dCos ); 21: p04.setX( p01.x() + dDist*dSin ); 22: p04.setY( p01.y() + dDist*dCos );
角の1点をドラッグして変形するには
回転した長方形の角の1点をドラッグして、長方形を保ったまま拡大/縮小したい場合、
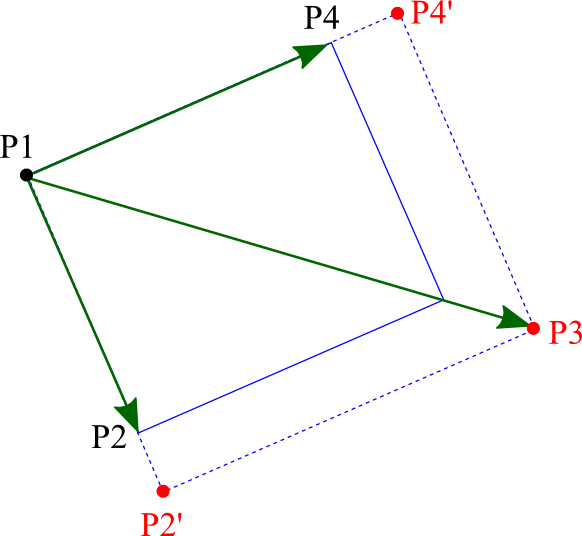
すなわち、図のようにP3が移動したときにP2’、P4’の座標を求めるには以下のようにします。
P3’に対応するP2’とP4’の位置は、まず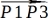 と
と
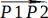 、
、
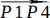 の内積をそれぞれ求め、
の内積をそれぞれ求め、
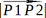 、
、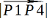 で内積の値を割ることで
で内積の値を割ることで
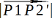 、
、
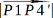 の値が求まります。
の値が求まります。
この長さを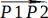 、
、
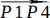 の単位ベクトルに掛ければいいので、
の単位ベクトルに掛ければいいので、
結果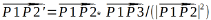 となります。
となります。
1: 2: // pPosが点Cに対応しているものとする 3: QPointF pPos; 4: 5: // rcが変更する矩形 6: // P1、P2、P3、P4の順で点が格納されているものとする 7: QRectF rc; 8: 9: // 各ベクトルを求める 10: QPointF vectL1 = rc[1] - rc[0]; 11: QPointF vectL2 = rc[3] - rc[0]; 12: QPointF vectL3 = pPos - rc[0]; 13: 14: // 長さ^2 15: double dLenL1 = pow(vectL1.x(), 2) + pow(vectL1.y(), 2); 16: double dLenL2 = pow(vectL2.x(), 2) + pow(vectL2.y(), 2); 17: 18: // 修正後の長さ 19: dLenL1 = (vectL1.x()*vectL3.x() + vectL1.y()*vectL3.y()) / dLenL1; 20: dLenL2 = (vectL2.x()*vectL3.x() + vectL2.y()*vectL3.y()) / dLenL2; 21: 22: // P2'とP4'の座標を求める 23: QPointF pntNewL1 = rc[0] + vectL1*dLenL1; 24: QPointF pntNewL2 = rc[0] + vectL2*dLenL2; 25: 26: // 矩形を修正 27: rc.set( 1, pntNewL1 ); 28: rc.set( 2, pPos ); 29: rc.set( 3, pntNewL2 );
