最尤法による画像分類
教師付き分類でおなじみの最尤法による画像分類は以下のようにして行います。
分類クラスに対する未知試料の尤度が正規分布で表されるとき、尤度は以下のように表されます。
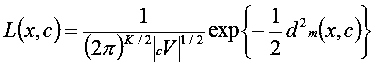
最尤法では、この尤度が最大のクラスに分類します。
マハラノビス距離dmは以下の式で求められます。

ここで、xXは入力ベクトル、cMはクラスcの平均ベクトル、
cVはクラスcの分散・共分散行列です。
式の形は、普通使うユークリッド距離の計算式の間に分散・共分散行列が挟まれている形です。
尤度の計算式は、実際は変形して簡単にした以下の式を用います。
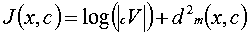
|cV|は分散・共分散行列の行列式です。
上式のJ(x,c)が最小のクラスに分類することになります。
最初の尤度の式と比較して符号が変わっている点が注意です。
下のサンプルは出力画像のピクセルにクラス番号を入れて返します。
/* RGB画像に対する最尤法による分類 btIn : 入力画像、1次元配列で8bitとしている btOut : 出力画像、1チャンネル nRow : 画像の縦ピクセル数 nCol : 画像の横ピクセル数 nCh : チャンネル数 nClass : 分類クラス数 daaMeanVect : 各分類クラスの平均ベクトル btClassColor : 各分類クラスの出力時の色 daDet : 各分類クラスの分散・共分散行列の行列式の値 daaaInvCoVar : 各分類クラスの分散・共分散行列の逆行列 ( クラス数 × チャンネル数 ) */ void classify_mlc ( BYTE *btIn, BYTE *btOut, int nRow, int nCol, int nCh, int nClass, double **daaMeanVect, double *daDet, double ***daaaInvCoVar ) { int i, j, k, l, m; double dDist, dMinJ, dMahal, dJ; int nNearestClass; double *daDet_log, *dDif_Mean, *daTemp; /* 各クラスの分散・共分散行列の行列式の値の対数を記録する */ daDet_log = (double *)malloc( nClass * sizeof( double ); for ( i = 0; i < nClass; i++ ) { dDet_log = log( daDet[i] ); } /* マハラノビス距離の計算 */ dDIf_Mean = (double)malloc( nCh * sizeof(double) ); dTemp = (double)malloc( nCh * sizeof(double) ); for ( i = 0; i < nRow; i++ ) { for ( j = 0; j < nCol; j++ ) { dMinJ = 0.99E+37; for ( k = 0; k < nClass; k++ ) { /* 平均ベクトルとの差を記録する */ for ( l = 0; l < nCh; l++ ) { dDif_Mean[l] = btIn[i*nCol*nCh+j*nCh+l] - daaMeanVect[k][l]; } /* 平均値ベクトルとの差 × 分散・共分散行列の逆行列 */ for ( l = 0; l < nCh; l++ ) { dTemp[l] = 0.0; for ( m = 0; m < nCh; m++ ) { dTemp[l] += daaaInvCoVar[k][l][m] * dDif_Mean[m]; } } /* マハラノビス距離を計算 */ dMahal = 0.0; for ( l = 0; l < nCh; l++ ) { dMahal += dDif_Mean[l] * dTemp[l]; } /* 決定数Jを求める */ dJ = dDet_log[nClass] + dMahal; if ( dJ < dMinJ ) { dMinJ = dJ; nNearestClass = k; } } for ( l = 0; l < nCh; l++ ) { btOut[i*nCol+l] = nNearestClass; } } } free( daDet_log ); free( dDif_Mean ); free( dTemp ); }
