IDW（Inverse Distance Weighting）

逆距離加重法と訳されることが多いようです。
IDWは、対象点xの値u(x)を、周辺N点x_iの値u(x_i) (i=0,1,…N)を使って、
以下の式で補間します。

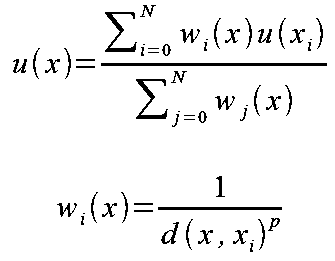
要は、距離の逆数を重みとした加重平均で値を求めることになります。近傍点の配点位置はまったく見ないので、外挿も可能です。

pの値は小さいほど近傍点の値の影響が大きくなります。通常は1（距離そのもの）～2（距離の２乗）を採用することが多いようです。
Nの値は1にすると近傍点のVoronoi分布で値を決定するのと同じになります。

IDW自体はこれだけのことで、それほど難しくありませんが、大変なのは近傍点をどうやって探すかです。
以下の例ではこちらのコードのk-d木を利用しています。
この場合、”N点以上”とするか”N点”とするかで手間が違います。
”N点”とする場合は、探し出した近傍点を距離順に並べなおす必要があります。
以下の例では、簡単に”N点以上”としています。

#include "../kdtree-0.5.5/kdtree.h"
#include <vector>

#define SEARCH_RANGE 10

typedef struct _point
{
	double dX;
	double dY;
	double dZ;
} POINT;

std::vector<POINT *> g_vPnt;
struct kdtree *g_pTree;

void CreateTree( int nDim )
{
	g_pTree = kd_create( 2 );
}

void AddDataToTree( POINT &pnt )
{
	POINT *pPnt;
	double dPos[2];

	pPnt = new POINT;

	memcpy( pPnt, &pnt, sizeof(POINT) );

	dPos[0] = pPnt->dX;
	dPos[1] = pPnt->dY;
	g_vPnt.push_back( pPnt );
	kd_insert( g_pTree, dPos, pPnt );
}

void ReleaseData()
{
	for ( int i = 0; i < g_vPnt.size(); i++ )
	{
		delete g_vPnt[i];
	}
	kd_free( g_pTree );
}

void DoIDW( POINT &sPnt, int nMinRef, int nPow )
{
	int nRes, nSearchMulti;
	int k;
	double dPos[2];
	struct kdres *res;
	double dTotDist1 = 0.0, dTotDist2 = 0.0, dDist;
	POINT **ppResPnt;

	dPos[0] = sPnt.dX;
	dPos[1] = sPnt.dY;

	nRes = 0;
	nSearchMulti = 1;
	while ( true )
	{
		res = kd_nearest_range( g_pTree, dPos, nSearchMulti*SEARCH_RANGE );
		nRes = kd_res_size( res );
		if ( nRes >= nMinRef )
		{
			break;
		}
		nSearchMulti++;
		kd_res_free( res );
	}

	// Search nearest
	dTotDist1 = dTotDist2 = 0.0;
	ppResPnt = new POINT*[nRes];
	k = 0;
	while ( !kd_res_end( res ) )
	{
		ppResPnt[k] = (POINT *)kd_res_item( res, NULL );
		if ( ppResPnt[k]->dX == dPos[0] && ppResPnt[k]->dY == dPos[1] )
		{
			sPnt.dZ = ppResPnt[k]->dZ;
			break;
		}

		// IDW
		dDist = sqrt( (ppResPnt[k]->dX-dPos[0])*(ppResPnt[k]->dX-dPos[0]) + (ppResPnt[k]->dY-dPos[1])*(ppResPnt[k]->dY-dPos[1]) );
		dTotDist1 += ppResPnt[k]->dZ / pow( dDist, nPow );
		dTotDist2 += 1 / pow( dDist, nPow );

		kd_res_next( res );
		k++;
	}

	sPnt.dZ = dTotDist1 / dTotDist2;
	delete[] ppResPnt;

	kd_res_free( res );
}

上記のコードを使って、ランダム点からDEMを作成した結果を以下に示します。

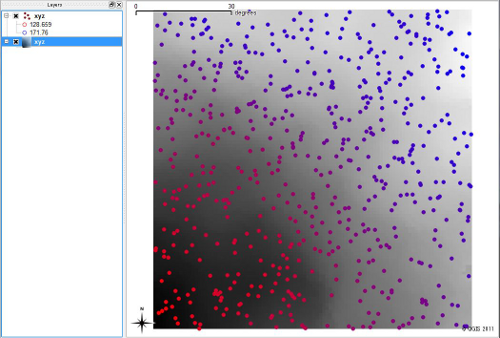
実行結果（N=4、p=1）

参考文献

• • Inverse distance weighting – Wikipedia,
    the free encyclopedia

• • Inverse distance
    weighting (IDW)

• • kdtree – A simple C library for working with KD-Trees – Google
    Project Hostin

• • GRASSコード　vector/v.surf.idw/main.c